A. Plotting overview (review from last lesson)
-
MATLAB has an extensive set of plotting functions. We will only present an overview of MATLAB's capabilities. If you are interested in learning all of the possible plotting features in MATLAB, search for "Specialized Plotting" in MATLAB's help system.
-
MATLAB functions for generating plots (a subset)
Plot type 2D Plots 3D Plots line graphs plot(), ezplot(), fplot()
semilogz(), semilogy(), loglog()plot3(), ezplot3() scatter plots (graph) scatter() scatter3() histograms (graph) hist(), histc() bar charts bar(), barh() bar3(), bar3h() pie charts pie() pie3() surface plots (graph) surf() mesh plots (graph) mesh() contour plots (graph) contour() contour3() - This lesson will concentrate on the plotting of commonly used graphs and charts.
B. Pie Charts
- The pie() function will create a pie
chart that represents the percentages of the whole from a
row vector of data values. The pie()
function calculates the sum of all values in the vector and then divides
each individual value by this sum to calculate the percentage of each
value in the vector.
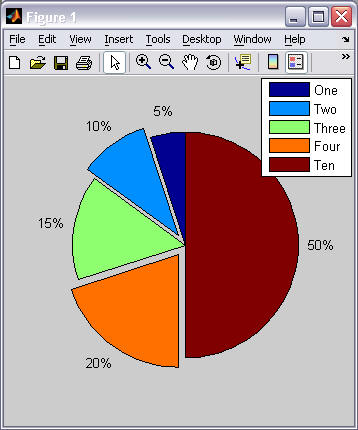
Example 1 Example 2 % pie(vector) pie( [1 2 3 4 10] )
legend('One', 'Two', 'Three', 'Four', 'Ten')% pie(vector, exploded) pie([1 2 3 4 10], [0 1 0 1 0])
legend('One', 'Two', 'Three', 'Four', 'Ten')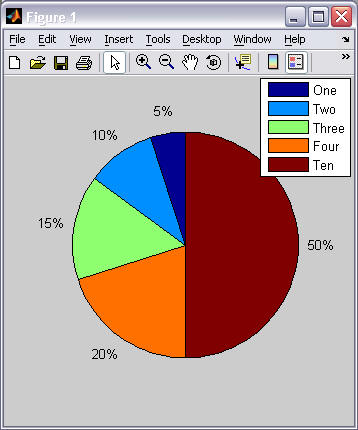
B. Bar Charts
- The bar() and
barh() functions will create a bar
chart. Bar charts are typically used to represent the comparison of
discrete categories of data. To label the bars in the chart requires the
use of the set() and
gca() functions in combination with the
'XTickLabel' axes property. These
functions will be described in more detail later in the course. For now,
just use the example statements shown below and modify the labels as
needed.
Example 1 Example 2 % bar(vector) bar([23 34 12 45]);
set(gca(), 'XTickLabel', ...
{'DFC', 'DFMS', 'DFM', 'DFCS'});
% barh(vector) barh([23 34 12 45]);
set(gca(), 'YTickLabel', ...
{'DFC', 'DFMS', 'DFM', 'DFCS'});
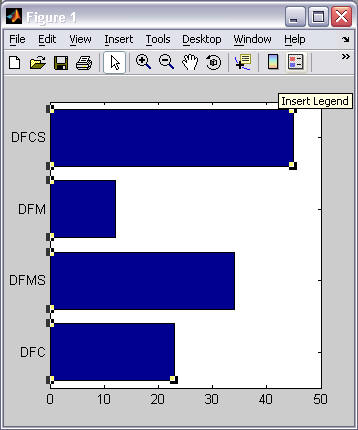
- If you are comparing multiple values for each discrete category,
provide a 2D matrix for the bar() function, where the multiple values
for each category are in the same row of the 2D array. Refer to the
examples below.
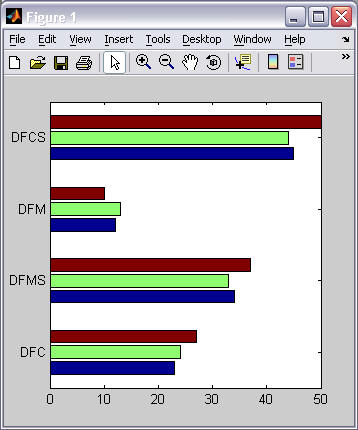
Example 3 Example 4 % bar(matrix) bar([23 24 27; ...
34 33 37; ...
12 13 10; ...
45 44 50]);
set(gca(), 'XTickLabel', ...
{'DFC', 'DFMS', 'DFM', 'DFCS'});
% barh(matrix) barh([23 24 27; ...
34 33 37; ...
12 13 10; ...
45 44 50]);
set(gca(), 'YTickLabel', ...
{'DFC', 'DFMS', 'DFM', 'DFCS'});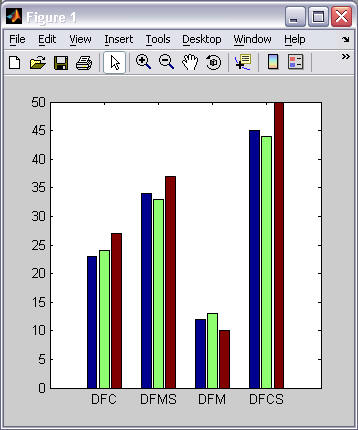
C. Histograms (graphs)
- The hist() function will create a
histogram -- a graph of the distribution of values within a data set.
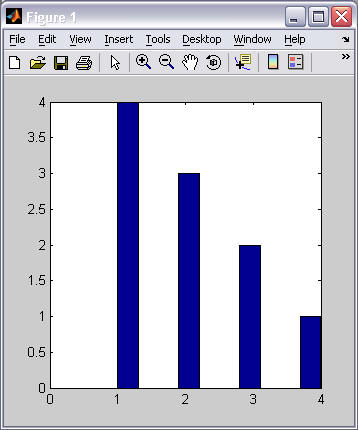
Example 1 Example 2 % hist(vector) hist( [1 2 3 4 1 2 3 1 2 1] );
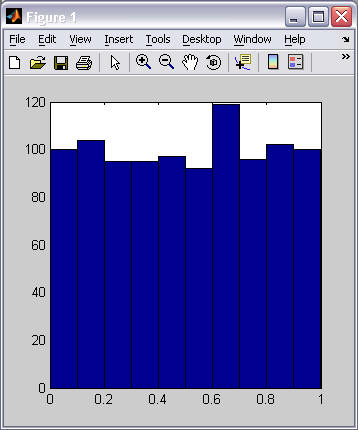
% hist(vector) hist( rand(1,1000) );
- The number of groupings (called bins) used for a histogram
distribution can be specified in one of two ways:
- How many bins to use.
- A vector that specifies the "center point" of each bin. (The limits of each bin is determined by the half-way points between each specified "center point". The first and last bin is always symmetrical around its "center point" -- which may exclude values in the lower and upper ranges of your data if the bins are not equally spaced. If you specify a "center point" vector, you typically want the "center points" to be symmetrically spaced along the horizontal axis.)