CSCE 310 Data
Structures & Algorithms
Fall 2004
Steve Goddard
1. Illustrate the operation of merge sort on the array A = (3, 41, 52, 26, 38, 57, 9, 49). Show each level of recursion in your work.
2. You have studied the binary heap. Consider a ternary heap, where each non-leaf node has 3 children instead of 2. What is the height of this heap in terms in terms of n?
3. Prove
by induction on n that 
. Similarly, prove by
induction k that
.
4. Explain the effect of both an algorithms’ constant factor and it’s asymptotic growth. Give a numerical example that shows the conditions where each factor dominates.
5. What is the primary purpose of presenting the ADT methodology? What are other advantages?
6. List in order of most general to most specialized, the following data structures: Indicate where they could be considered into be on the same level. Give reasoning for your ranking and how the level becomes more specialized.
Binary tree, tree, AVL tree, binary search tree, heap, priority queue.
7. Indicate how a stack and a queue differ from each other. How are they the same? Give an example of an application in which they would be used.
8. Give a definition of height and depth when used in conjunction with a binary tree. How are the two terms different?
9. Consider recursion and mathematical induction. How can the two be seen to be related?
10. When traversing a tree, there are three methods of doing this: pre-order, in-order, and post-order. Draw a tree of at least height 4 and give the traversal using each of these three methods. To make the exercise meaningful, make each node of the tree unique.
11. How does quick sort differ from merge sort? They both divide an array, so what’s the difference? Give aspects of asymptotic growth, space usage and any other feature where they can be compared.
12. A 2-3 tree will help reduce search time when compared to a regular binary tree. How is this done? Compare attributes of the two types of trees, considering best case and worst-case situations.
13. When is an open addressing has table preferable to a closed address hashing table? Consider load factors and size of element in your answer.
14. You have studied both directed graphs and undirected graphs. When is one used over the other?
How do the definitions of a cycle differ between the two?
15. There are two general forms for implementing a graph: An adjacency matrix and an array of adjacency list. When is one more desirable to use in an implementation, over the other? Consider graph size and satellite data in your answer.
16. Draw a diagram that shows how the following types of problems are related: NP, NP-hard, P, NP-complete. Define the progress or relation between the types.
17. In the graph below, give the strongly connected components. Indicate either your reasoning or the algorithm you followed to determine this. Be complete.
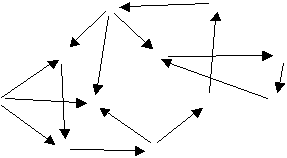t u
v w x
y z { |
} ~
18. Perform a left hand rotation about the node labeled 2. Draw out the resulting tree, clearly marking all nodes.
t
u v
x y {
z |
}